PERSAMAAN DAN TIDAK PERSAMAAN EKSPONENSIAL

Persamaan Eksponen

Persamaan eksponen ditandai dengan dua fungsi bilangan berpangkat yang dihubungkan dengan tanda sama dengan (=). Misalnya terdapat sebuah bilangan dengan pangkat sebuah fungsi linear dan hasilnya yaitu 32x – 1 = 1. Persamaan tersebut merupakan contoh persamaan eksponen. Hasil dari persamaan tersebut adalah nilai x yang memenuhi persamaan tersebut.

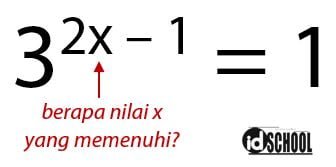
Nilai x yang memenuhi persamaan eksponen pada contoh di atas adalah x = ½. Susbtitusi nilai x = ½ ke dalam persamaan akan menghasilkan 30 = 1. Dari mana nilai x tersebut diperoleh? Untuk menyelesaikan persamaan eksponen, sobat idschool perlu mengetahui sifat – sifat yang berlaku pada persamaan eksponen.

Daftar sifat – sifat persamaan eksponen diberikan seperti berikut.

• a0 = 1
• a–1 = 1/a
• am × an = am + n
• am : an = am – n
• (am)n = am × n
• (am × an)p = apm + pn

Selain mengetahui sifat – sifat eksponen seperti yang diberikan pada bahasan di atas, sobat idschool juga perlu mengetahui sifat fungsi eksponen. Beberapa sifat fungsi eksponen diberikan pada daftar berikut.

• Jika af(x) = ap maka f(x) = p
• Jika af(x) = ag(x) maka f(x) = g(x)

Sifat – sifat pada eksponen dan sifat fungsi eksponen akan membantu sobat idshool dalam menyelesaikan soal persamaan eksponen. Sekarang perhatikan kembali contoh yang diberikan di awal, yaitu 32x – 1 = 1.

Proses mendapatkan nilai x = 1/2 dapat dilihat pada contoh cara menyelesaikan persamaan eksponen berikut.

32x – 1 = 1
32x – 1 = 30
2x – 1 = 0
2x = 1
x = 1/2

Baca Juga: Pengertian Eksponen

Pertidaksamaan Eksponen

Cara menyelesaikan pertidaksamaan eksponen hampir sama dengan penyelesaian persamaan eksponen. Karakteristik dari pertidaksamaan eksponen dengan dua fungsi bilangan berpangkat yang dihubungkan tanda pertidaksamaan. Bentuk tanda pertidaksamaan tersebut dapat berupa lebih besar (>), lebih besar/sama dengan (≥), lebih kecil (<), atau lebih kecil/sama dengan (≤). Contoh pertidaksamaan eksponen adalah 32x – 1 < 1.

Untuk menyelesaikan soal pertidaksamaan tersebut, sobat idschool juga perlu mengenali beberapa sifat yang berlaku pada pertidaksamaan eksponen.

• Untuk a ≥ 1:
  af(x) > ag(x) → f(x) > g(x)
  af(x) ≥ ag(x) → f(x) ≥ g(x)
  af(x) < ag(x) → f(x) < g(x)
  af(x) ≤ ag(x) → f(x) ≤ g(x)

• Untuk 0 < a < 1:
  af(x) > ag(x) → f(x) < g(x)
  af(x) ≥ ag(x) → f(x) ≤ g(x)
  af(x) < ag(x) → f(x) > g(x)
  af(x) ≤ ag(x) → f(x) ≥ g(x)

Perhatikan contoh menyelesaikan pertidaksamaan eksponen 32x – 1 < 1:

32x – 1 < 1
32x – 1 < 30
2x – 1 < 0
2x < 1
x < 1/2

Jadi, nilai x yang memenuhi pertidaksamaan 32x – 1 < 1 adalah x < 1/2

Perbedaan antara persamaan dan pertidaksamaan eksponen terdapat pada hasil akhirnya. Pada persamaan eksponen hasi akhir penyelesaiannya berupa suatu bilangan. Sedangkan hasil akhir dari pertidaksamaan eksponen hasil akhirnya berupa suatu daerah yang memenuhi pertidaksamaan

Contoh 1 – Soal Persamaan Eksponen

Pembahasan:

Mencari nilai x yang memenuhi dari persamaan eksponen yang diberikan pada soal.

Diketahui bahwa nilai p > q, maka nilai p = 1 dan q = – 1/3. Jadi, nilai p + 6q = 1 + 6(– 1/3)=1 – 2 = –1.

Jawaban: E

Contoh 2 – Soal Pertidaksamaan Eksponen

Himpunan penyelesaian dari pertidaksamaan eksponen

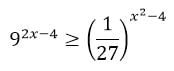
adalah ….
A. { x | –2 ≤ x ≤ 10/3}
B. { x | –10/3 ≤ x ≤ 2}
C. { x | x ≤ –10/3 atau x ≥ 2}
D. { x | x ≤ –2 atau x ≥ 10/3}
E. { x | –10/3 ≤ x ≤ –2 }

Pembahasan:

Menyelesaikan pertidaksamaan:

Pembuat nol: 3x2 + 4x – 20 = 0

Menyelesaikan persamaan kuadrat:

3x2 + 4x – 20 = 0
(3x + 10)(x – 2) = 0
3x + 10 = 0 atau x – 2 = 0
x = –10/3  atau  x = 2

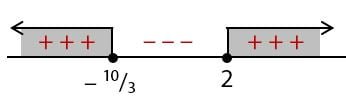
Menentukan daerah penyelesaian yang memenuhi pertidaksamaan:

Baca Juga: Pertidaksamaan Kuadrat dan Himpunan Penyelesaiannya

Dengan melakukan uji daerah pada garis bilangan akan diperoleh daerah yang menghasilkan nilai positif dan negatif. Selanjutnya dapat diperoleh penyelesaian dari pertidaksamaan yang diberikan pada soal adalah x ≤ –10/3  atau  x ≥ 2.